 |
Gamedev Framework (gf)
0.4.0
A C++11 framework for 2D games
|
 |
Gamedev Framework (gf)
0.4.0
A C++11 framework for 2D games
|
gf provides common functions and constants that are not in the standard library.
The gf::square() function computes the square of an expression. Squaring is a common operation and is better done doing a simple multiplication (instead of calling std::pow). When you have a simple variable, it is easy. But when you have an expression, it's a bit complicated and error-prone. Hence this simple but useful function.
\[ \text{square}(x) = x^2 \]
The gf::lerp() function computes a linear interpolation between two numbers. If you want a smoother interpolation, you can replace the last parameter with a call to a step function with this parameter (see Step functions).
\[ \text{lerp}(x_1, x_2, t) = (1 - t) * x_1 + t * x_2 \]
The gf::clamp() function computes the nearest value in a range. It can be used when a computation gives a value that may sits oustside a given range \( [l, h] \). In this case, a clamp puts the value inside the range.
\[ \text{clamp}(x, l, h) = \begin{cases} l & \text{if $x < l$} \\ h & \text{if $x > h$} \\ x & \text{otherwise} \end{cases} \]
The gf::sign() function computes the sign of a number (float or integer) and returns an integer reflecting that sign.
\[ \text{sign}(x) = \begin{cases} -1 & \text{if $x < 0$} \\ 0 & \text{if $x = 0$} \\ 1 & \text{if $x > 0$} \end{cases} \]
A step \( f \) is a (mathematical) function which has the following properties:
It can be used to smooth a linear interpolation. Step functions may have additional properties (especially regarding derivatives).
Here are the step functions that are provided by gf:
| Function | Implementation | Plot |
|---|---|---|
| gf::linearStep() | \( f(t) = t \) | 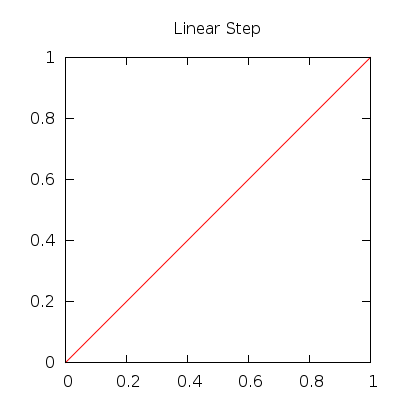
|
| gf::cubicStep() | \( f(t) = -2 * t^3 + 3 * t^2 \) | 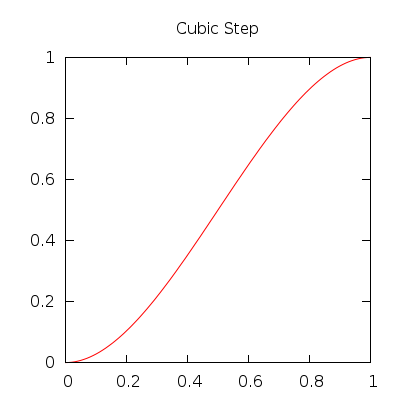
|
| gf::quinticStep() | \( f(t) = 6 * t^5 - 15 * t^4 + 10 * t^3 \) | 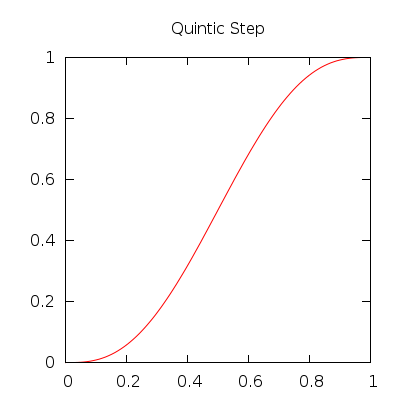
|
| gf::cosineStep() | \( f(t) = (1 - \cos(\pi * t)) * 0.5 \) | 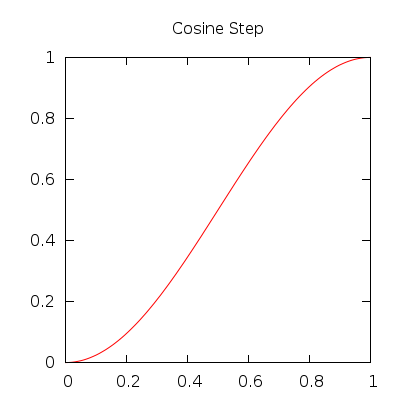
|
The type gf::Step is a function pointer to a step function.
gf has some other useful functions.
gf::almostEquals() compares two floats taking into account the rounding errors. This function takes care of many cases.
gf::degreesToRadians() and gf::radiansToDegrees() helps in converting angles from degrees to radians and from radians to degrees. These functions are defined as constepxr so you can use them for the initialisation of any variable without any runtime cost.
gf provides several common mathematical constants. All these constants are defined as constexpr so that they can be used in other constexpr expressions. The following table shows all the constants, their value and the approximation used in gf. The constants without an approximation are defined with another constant directly.
| Constant | Value | Approximation |
|---|---|---|
| gf::Pi | \( \pi \) | \( 3.14159265358979323846 \) |
| gf::Pi2 | \( \frac{\pi}{2} \) | |
| gf::Pi4 | \( \frac{\pi}{4} \) | |
| gf::Sqrt2 | \( \sqrt{2} \) | \( 1.41421356237309504880 \) |
| gf::InvSqrt2 | \( \frac{1}{\sqrt{2}} \) | |
| gf::Sqrt3 | \( \sqrt{3} \) | \( 1.7320508075688772935 \) |
A special constant is defined for floating point computation: the machine epsilon, noted \( \varepsilon \). In gf, it can be accessed with gf::Epsilon. It is defined thanks to std::numeric_limits but is more easily accessible.
 1.8.8
1.8.8